Square Puzzle

There are TV-shows around, that try to get the money of the onlooker by animating them to call expensive phone numbers to solve a puzzle, that looks easy.

One of the puzzle consists of a few points, and the question is, how many squares can you create by connecting 4 points together.

point matrix 4x3

Let's take a look at it. Yes, it is easy to see the small squares with an edge length of 1.

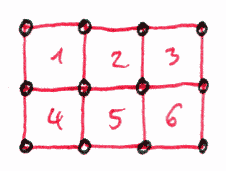
point matrix with marked squares edge=1

And even the two other with and edge length of 2 are easy to find.

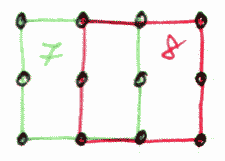
point matrix with marked squares edge=2

But nearly nobody of the onlookers see the squares, which can be created by connecting points in an other angle than 90°. In this case there are 2 additional one in an 45° angle.

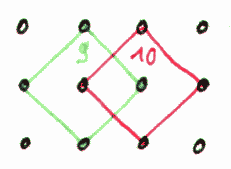
point matrix with marked squares angle=45°



To demonstrate how the puzzle can be easily solved with an computer I've written a few lines of C-Code which can count the squares inside a textfile. The 'x' is used to mark the points.

Example:

 xxx  xxx
xxxxxxxxxx
xxxxxxxxxx
xxx    xxx
 xx xx xx
 xx xx xx
xxx    xxx
xxxxxxxxxx
xxxxxxxxxx
 xxx  xxx

Try to count the number of squares by hand first.

Listing of the program result (4 coordinates and the result number):
(2.0,-1.0), (1.0,-2.0), (2.0,-3.0), (3.0,-2.0)  solution 1
(2.0,-1.0), (2.0,-2.0), (3.0,-2.0), (3.0,-1.0)  solution 2
(2.0,-1.0), (1.0,-3.0), (3.0,-4.0), (4.0,-2.0)  solution 3
......
(3.0,-9.0), (3.0,-10.0), (4.0,-10.0), (4.0,-9.0)  solution 281
(7.0,-9.0), (7.0,-10.0), (8.0,-10.0), (8.0,-9.0)  solution 282
(8.0,-9.0), (8.0,-10.0), (9.0,-10.0), (9.0,-9.0)  solution 283

The program says that there are 283 squares. Unbelievable isn't it.

Download:

The license is public domain, so do whatever you want. This program comes with no warranty.

The programming language is ANSI-C.
The natural language is english.
OS independant.
Source-Code: square.c

back to the index page
created with quanta 3.1, werner.ho(AT)gmx.de 2003-06-20